DMZ - IT ¦ Matthias Walter
Stellen Sie sich vor, Sie möchten jemandem eine geheime Nachricht schicken – etwa eine Liebeserklärung oder ein Geschäftsgeheimnis – und das über das Internet, wo Hacker, Spione oder neugierige Nachbarn mithören könnten. Wie stellen Sie sicher, dass nur der Empfänger Ihre Nachricht lesen kann?
Hier kommt ein faszinierendes Verfahren ins Spiel, das wie digitale Magie wirkt: der Diffie-Hellman-Schlüsselaustausch. Dieser Mechanismus ermöglicht es zwei Personen, die sich nie begegnet sind, einen geheimen Schlüssel zu erstellen, mit dem sie ihre Nachrichten verschlüsseln können. Aber wie funktioniert das, und warum ist es so sicher? Lassen Sie uns das Schritt für Schritt erkunden – keine Sorge, wir halten es einfach und verständlich!
Ein geheimer Schlüssel über unsichere Kanäle
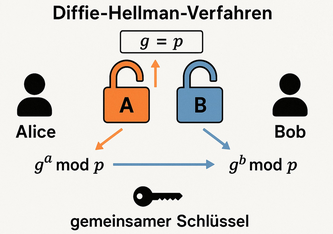
Das Internet ist wie ein riesiges, öffentliches Postsystem: Jeder kann Ihre Briefe sehen, wenn sie nicht verschlüsselt sind. Der Diffie-Hellman-Schlüsselaustausch löst dieses Problem, indem er zwei Personen – sagen wir Alice und Bob – erlaubt, einen gemeinsamen, geheimen Schlüssel zu erstellen, ohne dass ein Angreifer ihn herausfinden kann. Dieser Schlüssel wird dann verwendet, um Nachrichten zu verschlüsseln, sodass nur Alice und Bob sie lesen können.
Das Verfahren ist genial, weil es auf einem mathematischen Trick basiert, der selbst für die leistungsstärksten Computer der Welt fast unlösbar ist. Dieser Trick heißt „diskreter Logarithmus“. Keine Panik, wir erklären das ohne komplizierte Formeln!
So funktioniert Diffie-Hellman
Stellen Sie sich Alice und Bob vor, die sich auf eine geheime Kommunikation vorbereiten. Hier ist, wie sie vorgehen:
Öffentliche Zutaten wählen: Alice und Bob einigen sich auf zwei Zahlen, die jeder kennen darf – nennen wir sie „Grundzahl“ und „Modul“. Diese Zahlen sind wie die Zutaten für ein Rezept, das jeder sehen kann. Zum Beispiel könnten sie die Zahlen 5 (Grundzahl) und 23 (Modul) wählen.
Geheime Zutat hinzufügen: Jede Person wählt eine eigene, geheime Zahl, die niemand sonst kennt. Alice entscheidet sich für 6, Bob für 15. Diese Zahlen sind wie geheime Gewürze, die nur sie kennen.
Mischung austauschen: Alice berechnet eine neue Zahl, indem sie die Grundzahl (5) mit ihrer geheimen Zahl (6) verknüpft: 5 hoch 6, geteilt durch 23, ergibt 8 (genauer: 5^6 mod 23 = 😎. Bob macht dasselbe mit seiner geheimen Zahl: 5 hoch 15, geteilt durch 23, ergibt 19. Diese Ergebnisse (8 und 19) schicken sie sich gegenseitig über das Internet. Ein Hacker, der mithört, sieht also nur die Zahlen 8 und 19.
Geheimen Schlüssel berechnen: Jetzt kommt der magische Moment. Alice nimmt Bobs Zahl (19) und verknüpft sie mit ihrer geheimen Zahl (6): 19^6 mod 23 = 2. Bob nimmt Alice’ Zahl (😎 und verknüpft sie mit seiner geheimen Zahl (15): 8^15 mod 23 = 2. Beide kommen zur gleichen Zahl: 2. Das ist ihr gemeinsamer, geheimer Schlüssel!
Warum ist das sicher?
Die Sicherheit von Diffie-Hellman liegt im Problem des „diskreten Logarithmus“. Ein Angreifer, der die öffentlichen Zahlen (5 und 23) und die ausgetauschten Zahlen (8 und 19) kennt, müsste herausfinden, welche geheimen Zahlen (6 und 15) verwendet wurden. Das klingt vielleicht machbar, ist aber unglaublich schwierig – selbst Supercomputer würden dafür länger brauchen, als das Universum alt ist! Der diskrete Logarithmus ist wie ein Schloss, für das es keinen Dietrich gibt.
Ein anschauliches Bild
Um das Ganze greifbarer zu machen, stellen Sie sich vor, Alice und Bob wollen eine geheime Farbe mischen. Sie einigen sich öffentlich auf eine Grundfarbe, sagen wir Gelb. Jeder fügt dann im Geheimen eine eigene Farbe hinzu – Alice mischt Blau dazu, Bob Rot. Sie schicken sich die gemischten Farben (die nur aus der Ferne sichtbar sind), und durch eine spezielle Technik können beide die gleiche Endfarbe herstellen. Ein Spion, der nur die gemischten Farben sieht, hat keine Chance, die geheime Endfarbe zu erraten.
Warum ist Diffie-Hellman so wichtig?
Der Diffie-Hellman-Schlüsselaustausch ist ein Eckpfeiler der modernen Kryptografie. Er wird in vielen Technologien verwendet, die wir täglich nutzen – von sicheren Online-Banking-Transaktionen über verschlüsselte WhatsApp-Nachrichten bis hin zu VPNs, die unsere Daten schützen. Ohne Diffie-Hellman wäre das Internet ein viel unsicherer Ort.
Fazit: Sicherheit durch Mathematik
Diffie-Hellman zeigt, wie elegant Mathematik unsere digitale Welt schützen kann. Mit einem simplen, aber genialen Verfahren können zwei Fremde einen geheimen Schlüssel erstellen, selbst wenn die ganze Welt mithört. Das nächste Mal, wenn Sie eine sichere Verbindung im Internet nutzen, denken Sie an Alice, Bob und den diskreten Logarithmus – die unsichtbaren Helden hinter Ihren verschlüsselten Nachrichten.“
Quellen:
Diffie, W., & Hellman, M. (1976). „New Directions in Cryptography“. IEEE Transactions on Information Theory, 22(6), 644–654.
Stinson, D. R. (2005). Cryptography: Theory and Practice. CRC Press.
Schneier, B. (1996). Applied Cryptography: Protocols, Algorithms, and Source Code in C. Wiley.

Kommentar schreiben